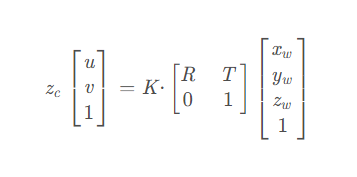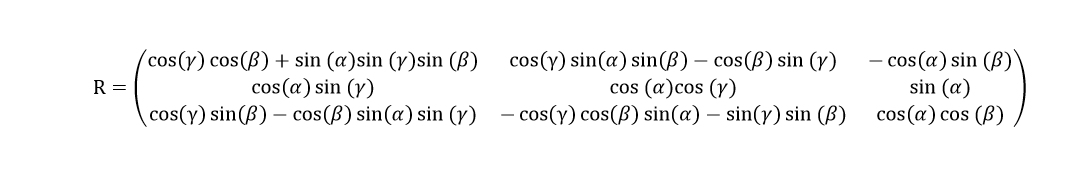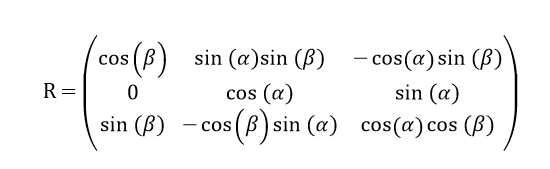引言
单目摄像头测距,这个课题既充满挑战,又极具有意义,因为没有昂贵的距离传感器而大幅度降低成本,潜力巨大。试想一下,普通的一个摄像头,只要进行简单的标定(只在画面上点几下),就能测算出画面中任意两个点之间的距离,是不是很方便呢?
先修知识
目前研究单目测距的领域主要还是集中在智能交通领域,由于交通上有几个先天的优势,使得研究更加容易:
一是车道线是平行线,这一点很容易保证;
二是车辆识别非常成熟,可以快速定位;
三是摄像头相对固定。
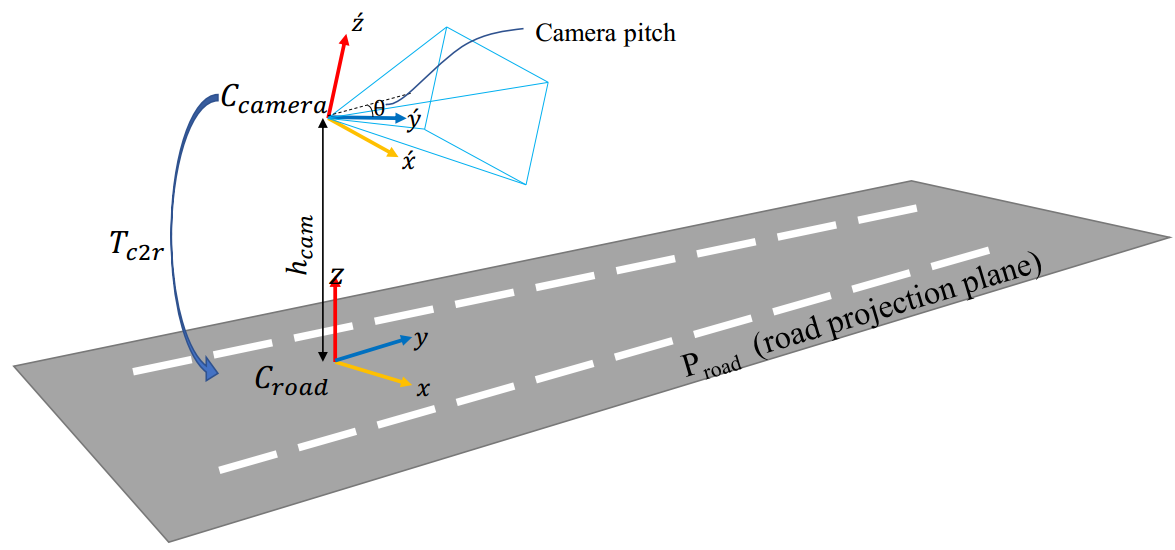
但是我们摄像头捕获的画面是一个平面,与真实世界坐标系之间需要做一次平移和一次旋转变换,下面这张图比较直观的展示了这个变换。
这个变换过程的讲解可以参考这篇博文,讲的非常详细: Step1:模型 16个相机参数(内参、外参、畸变参数)相机模型内在参数笔还是要动的的博客-CSDN博客 。其中,最重要的结论就是变换方程:
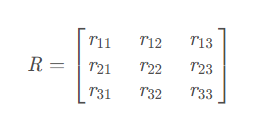
其中,K是相机内参矩阵,只跟相机本身出厂参数有关,后面是外参矩阵,由R(旋转矩阵)和T(平移矩阵)组合而来,Zc是比例系数
正文:
有了上面的结论,我们的问题转换成了已知u,v如何求解出世界坐标系下的x,y,w,很明显,这其实是一个数学问题,需要线性代数来帮忙。
先不要着急求解,我们的首要任务应该是先弄清楚K、R、T的值。
这里我们为了快速估算,作以下假设,假设道路监控摄像头的畸变忽略不计,这样我们可以得到fx = fy,u0=1/2W,v0=1/2H,其中W是画面宽度,H是画面高度。这样的话,K矩阵只剩fx这一个未知数。
如果是用欧拉角来表示的话,还可以写成这样:
其中,α是俯仰角,β是偏航角,γ是翻滚角,公式推导请参考: 欧拉角(Eular Angle)详解 – Deep Studio (p-chao.com) 和根据相机旋转矩阵求解三个轴的旋转角/欧拉角/姿态角 或 旋转矩阵与欧拉角(Euler Angles)之间的相互转换,以及python和C++代码实现相机外参数旋转矩阵 求旋转角度点亮~黑夜的博客-CSDN博客
单是看到这个矩阵,可能头有点大,但是考虑到实际情况,我们可以大大简化,道路监控摄像头由于安装的关系,翻滚角γ基本近似为0,那么cosγ = 1,sinγ = 0。此时矩阵R简化为
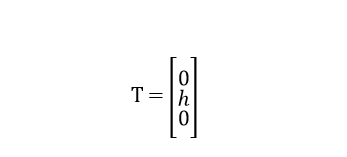
平移矩阵指的是从世界坐标系原点到相机坐标系原点的变换矩阵。放到这个监控图中,就是从路面到相机所在位置,平移的距离就是相机的安装高度。
这里安装高度我们假设是已知的。下面我们就来解这个方程。
如果直接去标定这几个角也是可以的,就是相对麻烦一点,有没有更简单的办法呢?答案是有的,就是利用图像消失点来计算。还是看这张图,由于车道线平行的关系,我们很容易就找到了其中一个消失点P:
详细的推导见: 如何通过图像消失点计算相机的位姿?_Being_young的博客-CSDN博客 ,这里给出结论:
这样的话,只要内参矩阵K和消失点P已知,就能解出俯仰角α和偏航角β,继而得到旋转矩阵R,结合已知的平移矩阵T,中间参数全部得到了,只差一个比例系数Zc,但是,内参矩阵这里很难确定,因为没有标定的条件。再来看一下这个方程:
如果没有其它条件,依然没法求解出Zc,在实际可能的情况中,我们可以利用先验知识,比如某种车型的车辆长度或者标识牌等,确定画面中两点之间的距离。比如左侧停在路边的小车,确定图像坐标P0到P1,对应的是实际的车长L,这样便得到7个方程8个未知数,依然没法解。
这里作者想到的一个方法是,利用计算机的性能优势,设置一个初始虚拟焦距F=0.01,再以步进方式递增到50,每次迭代一个值,就计算一遍K、R,求解出P0到P1的理论距离L1,利用车长L已知的先验条件,记录L1与L的误差,然后选取出最小误差所对应的虚拟焦距F0作为镜头的实际焦距,便得到了镜头所对应的近似内参矩阵K及旋转矩阵R。
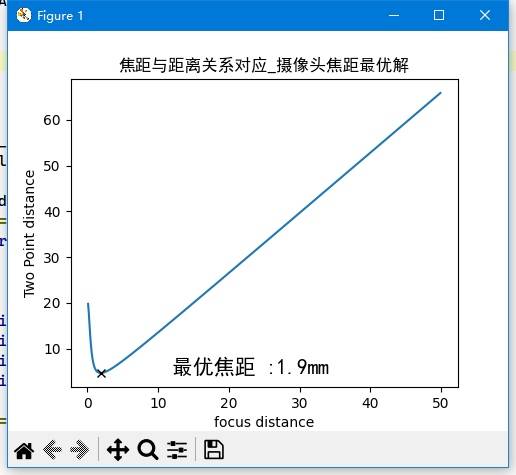
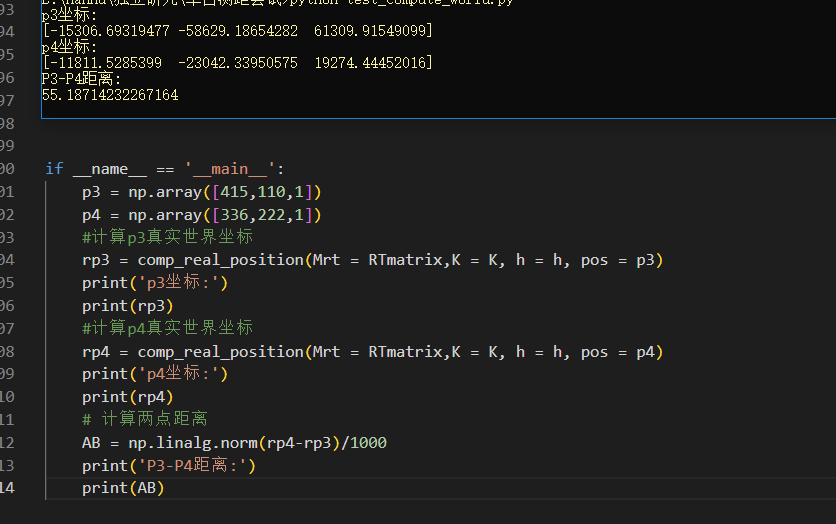
根据上述思想,写了对应的python脚本,输入上图中参数,预设了摄像头高度是6米,路边黑车车长4.5m,得到结果如下图:
这样,得到此摄像头虚拟焦距为1.9mm,代入到方程,即可求解任意坐标,写一个求解脚本,输入图像坐标,得到P3P4距离为55.18m。
这个结果有一定误差,经查询得知,标准高速的车行道分界面标准长度是6米,间隔9米,所以图中如果是标准划线的话,P3P4距离大概在30米。这里的误差作者认为主要来自于3个方面:
-
内参矩阵K忽略了畸变,以理想镜头代替;
-
摄像头安装高度为预估,实际可以简单测量一下;
-
参照物车辆的长度是以经验估计的,如果有更加精确的参照物,结果也会更加精确;
以上的分析是否合理,请大佬不吝赐教。
更新说明:
以上过程有两点需要改正,特此说明,一是是外参矩阵的求解,由世界坐标系变换到相机坐标系的过程中,我们直观上的感觉是相机原点从地面上向上移动了h高度,但实际上相机是先经过旋转再经过平移h,也就是说真正的平移矩阵应该是R*T,简单的推导过程如下:

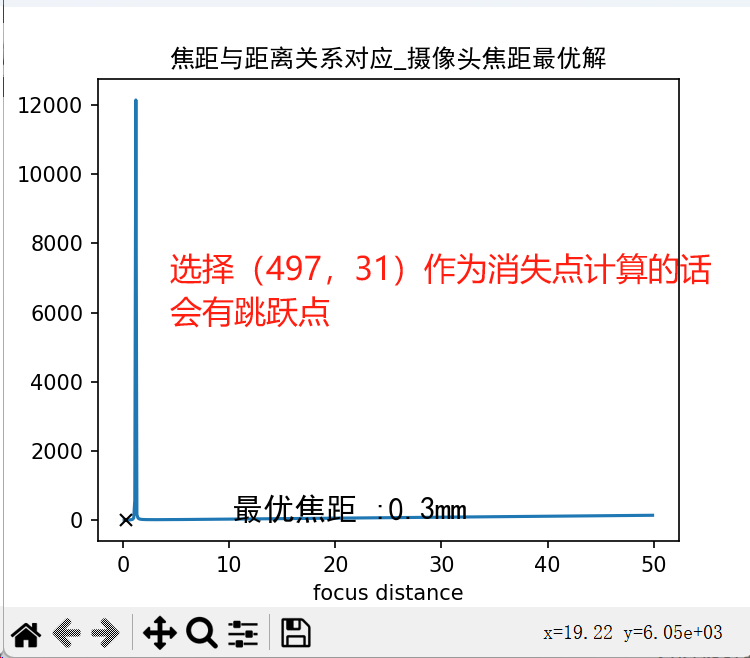
二是消失点的选取,之前是按实际理解直接选择了车道线的交点,理论上来说是没问题,但是考虑到这样处理实际上焦距曲线会有一个跳跃点,也就是说当在某个焦距下,两个点之间的距离会变成无穷大。
在光学中,当物体位于焦点位置时,其成像会出现特殊情况,即图像上的两点实际距离变成无穷大。
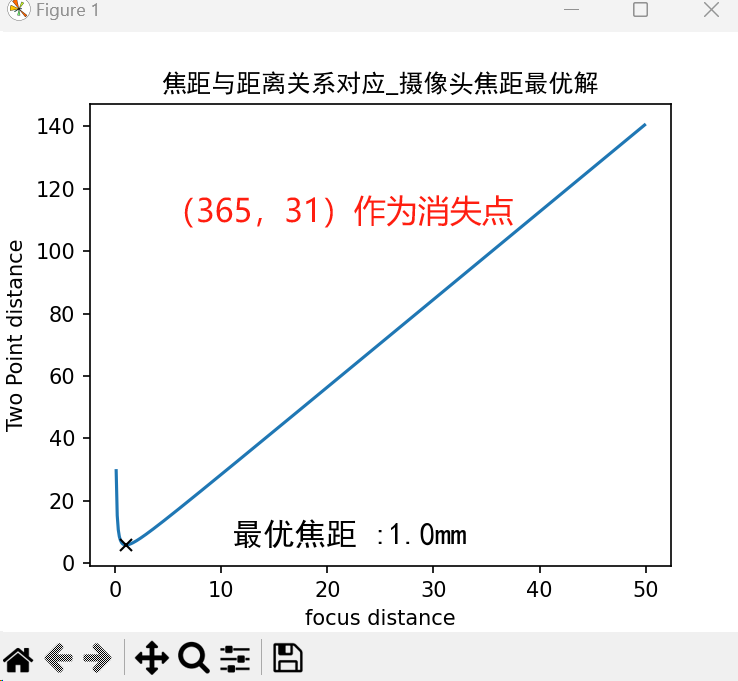
这里的处理方法就是直接选择地平线的中点为消失点,这样偏离理想焦距都会使得两点间的距离比实际距离更大,理想焦距就是最小值点的位置。
因此,代码作相应调整,得出此图焦距的最优解为1.0mm
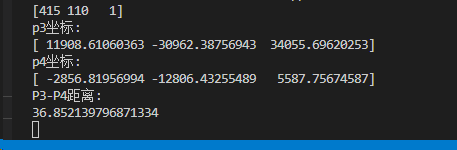
再重新代入外参矩阵,计算P3、P4之间的距离为36.8m,与实际距离更加接近。
验证这个内参矩阵和外参矩阵是否合理方法很多,这里可以这样做,计算从图像上每个点位出发到P4的距离,看最后距离图表是否和我们已知经验相一致。
从图片水平方向取100个点,垂直方向取50个点(需要注意的是由于地平线处距离非常大,如果从地平线处开始计算无法反应近处变化趋势,我们在可以在垂直方向点位取值从100到376),然后依次计算到p4点的距离,再使用matplotlib包画出3D曲面,得到曲面图如下:
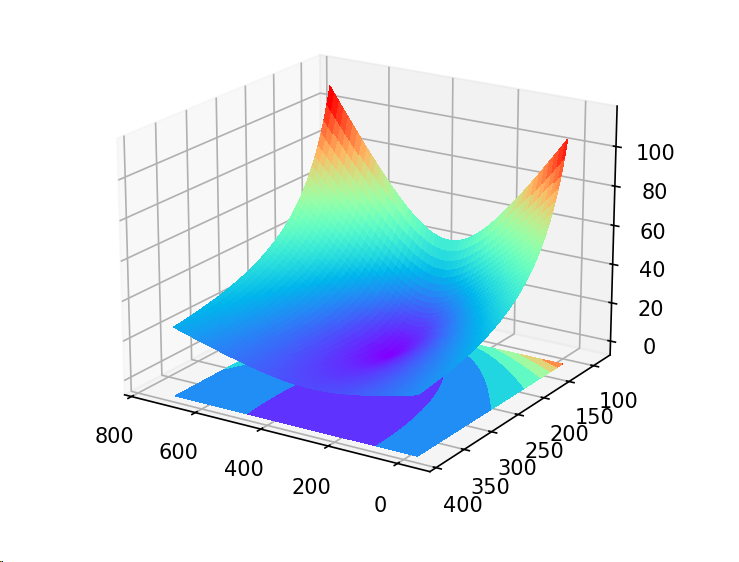

可以从3D图中清楚的看到,以P4为中心,点位与之距离逐渐增大,P4是极小值点,且值为0,原始图像垂直方向越靠近消失点距离变化越快,越靠近摄像机位置距离变化越小,这符合远小近大的物理规律。
(正文完)
主要代码:
from utils.k import Kmtrix
import numpy as np
import math
import matplotlib.pyplot as plt
# 获取f与距离关系,寻找最优解
def distance_list():
h = 6000 #单位mm
u0 = 365
v0 = 188
p0x = 365
p0y = 31
p1 = np.array([145,218,1])
p2 = np.array([192,18211])
a_list = []
b_list = []
f_list = []
dis_list = []
for f in range(1,500):
f= f / 10
# 计算内参矩阵
K = Kmtrix(f = f, u0= u0 , v0 = v0 )
# 计算旋转矩阵
a, b,Rmatrix = rotate_Matrix(p0x = p0x, p0y = p0y, K = K)
# 计算外参矩阵
RTmatrix = RT_Matrix(R = Rmatrix, h = h)
#计算p1真实世界坐标
rp1 = comp_real_position(Mrt = RTmatrix,K = K, h = h, pos = p1)
#计算p2真实世界坐标
rp2 = comp_real_position(Mrt = RTmatrix,K = K, h = h, pos = p2)
# 计算两点距离
AB = np.linalg.norm(rp2-rp1)/1000
a_list.append(a)
b_list.append(b)
f_list.append(f)
dis_list.append(AB)
return a_list,b_list,f_list,dis_list
def rotate_Matrix(*, p0x, p0y ,K):
K_1 = np.linalg.inv(K)
# 消失点在图像中坐标
P0 = np.array([p0x,p0y,1])
r3 = np.dot(K_1, P0)/np.linalg.norm(np.dot(K_1, P0))
# print(r3)
a = math.asin(r3[1])
# print(f'a='+str(a))
b= -math.atan(r3[0]/r3[2])
# print(f'b='+str(b))
# 旋转矩阵
R = np.array([
[math.cos(b), math.sin(a)*math.sin(b), -math.cos(a)*math.sin(b)],
[0, math.cos(a), math.sin(a)],
[math.sin(b), -math.cos(b)*math.sin(a), math.cos(a)*math.cos(b)]
])
return a,b,R
# 外参矩阵
def RT_Matrix(*, R, h):
T = np.array([0,h,0])
temp = np.concatenate((R ,np.dot( R , T.reshape(-1,1)),axis=1)
Mrt = np.concatenate((temp,np.array([[0,0,0,1]])),axis=0)
# print('Mrt')
# print(Mrt)
return Mrt
# 计算真实世界坐标
def comp_real_position(*,Mrt,K, h, pos):
K_E = np.concatenate((K , np.array([0,0,0]).reshape(-1,1)),axis=1)
M2 = np.dot(K_E, Mrt)
r1 = M2[:,0]
r2 = M2[:,1]
r3 = M2[:,2]
r4 = M2[:,3]
M3 = np.concatenate((r1.reshape(-1,1),pos.reshape(-1,1),r3.reshape(-1,1)),axis=1)
r5= -1 * h * r2 - r4
res = np.dot(np.linalg.inv(M3),r5)
return res
# 根据两点坐标,计算两点距离
def comp_distance(*, p1, p2):
p1 = comp_real_position(p1)
p1 = np.delete(p1,1,axis=0)
p2 = comp_real_position(p2)
p2 = np.delete(p2,1,axis=0)
# print('真实世界坐标:')
print(p1,p2)
AB = np.linalg.norm(p2-p1)
# print('两点距离(米):')
print(AB)
real_dis = 4.5
condition1 = lambda value: abs(value - real_dis)
if __name__ == '__main__':
a_list,b_list,f_list,dis_list = distance_list()
index = np.argmin([abs(estimate_dis - real_dis) for estimate_dis in dis_list])
print(dis_list[0])
print('最优焦距',f_list[index])
print('距离',dis_list[index])
print('index',index)
x = np.array(f_list)
y1 = np.array(dis_list)
fig=plt.figure(figsize=(5, 4), dpi=100)
plt.title('焦距与距离关系对应_摄像头焦距最优解',fontname="SimHei")
plt.xlabel('focus distance')
plt.ylabel('Two Point distance')
plt.plot(x,y1)
plt.plot(f_list[index], dis_list[index], "kx")
plt.text(f_list[index]+10,dis_list[index],'最优焦距 :'+ str(f_list[index])+'mm', fontsize=15,fontname="SimHei")
plt.show()
参考资料:
根据相机旋转矩阵求解三个轴的旋转角/欧拉角/姿态角 或 旋转矩阵与欧拉角(Euler Angles)之间的相互转换,以及python和C++代码实现相机外参数旋转矩阵 求旋转角度点亮~黑夜的博客-CSDN博客
基于车道线消失点的车距测量方法消失点测距公式海清河宴的博客-CSDN博客
单目3D目标检测论文笔记] 3D Bounding Box Estimation – 知乎 (zhihu.com)
欧拉角与旋转矩阵之间的转化公式及原理_欧拉角转旋转矩阵_LoongTech的博客-CSDN博客
欧拉角(Eular Angle)详解 – Deep Studio (p-chao.com)
透视没有那么难,就三点:地平线.消失点.视平线 (360doc.com)
如何通过图像消失点计算相机的位姿?_Being_young的博客-CSDN博客
Step1:模型 16个相机参数(内参、外参、畸变参数)相机模型内在参数笔还是要动的的博客-CSDN博客
Opencv中solvePnP函数的小结 – nikoooo – 博客园 (cnblogs.com)